Fungsi komposisi menjadi salah satu materi pelajaran Matematika yang harus dipahami oleh para siswa. Cara supaya lebih mudah memahami materi tersebut salah satunya dengan belajar contoh soal fungsi komposisi yang dilengkapi cara pengerjaan dan pembahasannya.
Pelajaran matematika memang penuh dengan rumus-rumus, termasuk contoh soal fungsi komposisi. Kalau siswa hanya menghafalkan rumusnya saja, sulit untuk bisa memahami dan mengerjakan soal dengan baik. Beda kalau langsung belajar dari contoh-contoh soal, siswa akan lebih mudah paham.
Apa Itu Fungsi Komposisi?
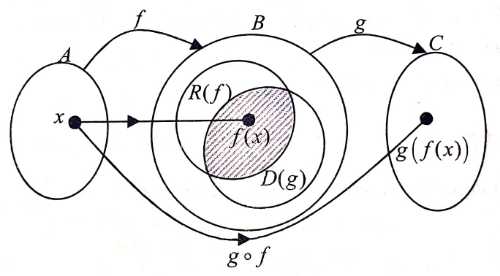
Fungsi komposisi dalam matematika memiliki pengertian penggabungan sebuah operasi yang terjadi diantara dua jenis fungsi, yaitu f(x) dan g (x), sehingga bisa menghasilkan sebuah fungsi yang baru.
Lambang fungsi komposisi di dalam matematika adalah “o” atau bundaran yang dibaca sebagai komposisi. Fungsi yang baru itulah yang dibentuk dari penggabungan antara f(x) dan g(x), yang artinya :
- (f o g)(x) dibaca sebagai g dimasukkan ke f
- (g o f)(x) dibaca sebagai f dimasukkan ke g
Pada penjelasan di atas, fungsi yang dilambangkan dengan (f o g) dibaca sebagai “f bundaran g” . Sedangkan (g o f)(x) dibaca sebagai “fungsi g bundaran f”.
Sifat Fungsi Komposisi
Fungsi komposisi di dalam materi pelajaran matematika memiliki sifat-sifat tertentu, yang akan berpengaruh pada cara penghitungan dan pembahasan contoh soalnya. Adapun sifat-sifat fungsi komposisi yaitu :
- Tidak berlaku atau tidak ada sifat komutatif, yaitu (f o g)(x) ¹ (g o f)(x)
- Tidak berlaku sifat asosiatif, yaitu (f o(g o h))(x) = ((f o g) o h)(x)
- Terdapat atau mengandung unsur identitas (f o l)(x) = (l o f)(x) = (f(x))
Syarat Fungsi Komposisi
Seperti sudah dijelaskan sebelumnya, bahwa pengertian fungsi komposisi dalam matematika adalah penggabungan pada sebuah operasi antara fungsi f(x) dan g(x), supaya dapat terbentuk sebuah fungsi yang baru.
Oleh karena itu, agar fungsi baru tersebut dapat dibentuk, maka ada persyaratan yang harus dipenuhi. Syarat yang dimaksud yaitu irisan antara daerah yang menjadi hasil dari fungsi f dan daerah asalh dari fungsi g, bukanlah termasuk himpunan kosong.
Adapun lambang syarat fungsi komposisi dinotasikan dengan Rf ∩ Dg¹Æ
Contoh Soal Fungsi Komposisi dan Pembahasannya
Agar lebih mudah dipahami oleh siswa, berikut ini diberikan beberapa contoh soal fungsi komposisi lengkap dengan cara mengerjakannya.
1. Jika f(x) = 2x + 2 dan g(x) = 6x2 . Maka (f o g)(x) dan (g o f)(x) adalah :
Jawaban :
(f o g)(x) = f (g(x))
(f o g)(x) = f (6x2)
(f o g)(x) = 2(6x2) + 2
(f o g)(x) = 12x2 + 2
(g o f)(x) = g(f(x))
(g o f)(x) = 6(2x + 2)2
(g o f)(x) = 6(4x2 + 12x + 4)
(g o f)(x) = 24x2 + 12x + 4
Jadi, (f o g)(x) = 12x2 + 2 dan (g o f)(x) = 24x2 + 12x + 4
2. Diketahui fungsi f:R→R dengan f(x)=8x+4 dan fungsi g g:R→R dengan g(x)= x – 2. Fungsi komposisi (fοg)(x) adalah :
Jawaban :
f(x)=8x+4
g(x)= x – 2
(fοg)(x) = f( g(x) )
= f( x-2 )
= 8(x-2) + 4
= 8x – 16 + 4
= 8x – 12
3. Fungsi f:R→R dan g:R→R dimana f(x)=4x-1 dan g(x)=x²+2. Tentukan (f ο g)(x)
Jawaban :
f(x)=2x-1
g(x)=x²+3
(f ο g)(x) = f( g(x) )
= f(x²+2)
= 4(x²+2) – 1
= 4x² + 8 – 1
= 4x² + 3
4. Diketahui fungsi f:R→R dengan f(x)=5x + 3 dan fungsi g:R→R dengan g(x)=x-2. Apakah (g ο f)(x) = (f ο g)(x)? Carilah jawabannya!
Jawaban :
Perlu diingat bahwa pada fungsi komposisi tidak berlaku sifat komutatif, jadi mari kita cari jawabannya berikut ini :
f(x) = 5x + 3
g(x) = x – 2
(g ο f)(x) = (f ο g)(x)
g( f(x) ) = f( g(x) )
g( 5x+3 ) = f( x-2 )
5x+3-2 = 4( x – 2) + 3
5x + 1 = 4x – 2 + 3
5x + 1 # 4x – 1
Karena 5x + 1 # 4x – 1 maka (g ο f)(x) # (f ο g)(x)
5. Jika f(x) = x² – 4 dan g(x) = 4x + 2 maka komposisi (f ο g)(x) adalah…
Jawaban:
f(x) = x² – 4
g(x) = 4x + 2
(f ο g)(x) = f( g(x) )
= f( 4x+2 )
= (4x+2)² – 4
= (4x²+4x+2) – 4
= 4x² + 4x – 2
6. Jika f:R→R dengan f(x)=x – 4dan g:R→R dengan g(x) = x² + 3. Tentukan (f ο g)(x-1)!
Jawaban:
f(x) = x – 4
g(x) = x² + 3
(f ο g)(x) = f( g(x) )
= f( x²+3)
= x² + 3 – 4
= x² – 1
(f ο g)(x-1) = (x-4)² – 1
= x² – 6x +9– 3
= x² – 6x + 6
7. Diketahui (f o g)(x) = 3x + 2 dan f(x) =x – 1. Tentukan fungsi g (x)
Jawaban :
(f o g)(x) = 3x + 2
f(g(x)) = 3x + 2
g(x) – 1 = 3x + 2
g(x) = 3x + 2 + 1
g(x) = 3x + 3
Jadi, fungsi g (x) adalah g(x) = 3x + 3
8. Tentukan f(x) jika (f o g)(x) = 4x + 5 dan g(x) = 2x + 4
Jawaban :
(f o g)(x) = 4x + 5
f(g(x)) = 4x + 5
f (2x + 4 = 4x + 5
f (u) = 4(½(u-4)) + 5
f (u) = 2u – 2 + 5
f (u) = 2u – 3
f (x) = 2x – 4
Jadi, fungsi f(x) = 2x – 4.
Misal u = 2x + 4, maka x = ½(u-4), sehingga:
f (2x + 4) = 4x + 5
f (u) = 4(½(u-4)) + 5
f (u) = 2u – 2 + 5
f (u) = 2u – 3
9. Jika f(x) = 3x, g(x) = 4x – 2, dan h(x) = x2, maka (f o g o h) (x) adalah :
Jawaban :
(f o g o h) (x) = (f o (g o h) (x))
(f o g o h) (x) = f (g (h(x))
(f o g o h) (x) = f (4(x2) – 2)
(f o g o h) (x) = f (4x2 – 2)
(f o g o h) (x) = 3 (4x2 – 2)
(f o g o h) (x) = 12x2 – 6
Jadi, (f o g o h) (x) = 12x2 – 6
10. Diketahui f(x) = x + 4 dan g(x) = 2x – 4. Tentukan (g o f)-1 (x)
Jawaban :
(g o f)-1 (x) = (f-1 o g-1) (x)
(g o f)-1 (x) = (f-1 (g-1(x))
Tentukan fungsi f-1(x):
f(x) = x + 4
y = x + 4
x = y – 4
f-1(x) = x – 4
Tentukan fungsi g-1(x):
g(x) = 2x – 4
y = 2x – 4
2x = y + 4
x = ½y + 2
g-1(x) = ½x + 2
Substitusikan f-1 (x) dan g-1 (x) ke (g o f)-1 (x) :
(g o f)-1 (x) = (f-1 (g-1(x))
(g o f)-1 (x) = f-1 (½x + 2)
(g o f)-1 (x) = (½x + 2) – 4
(g o f)-1 (x) = ½x -2
Jadi, (g o f)-1 (x) = ½x -2
11. Diketahui fungsi f(x) = 4x – 2, g(x) = 3x + 2 dan (f ο g)(a) = 75. Berapakah nilai a!
Jawaban :
f(x) = 4x – 2
g(x) = 3x + 2
(f ο g)(a) = 75
f( g(a) ) = 75
f(3a + 2) = 75
4(3a + 2) – 2 = 75
12a + 8 – 2=75
12a + 6= 75
12a = 69
a = 5,75
Jadi, nilai a yaitu 5,75
12. Jika f:R→R dengan f(x)=x³ + 2 dan g:R→R dengan g(x) = 4 sin x. Tentukan nilai (f ο g)(- 1/2 π)!
Jawaban :
f(x)=x³ + 2
g(x) = 4 sin x
(f ο g) (x) = f( g(x) )
= f( 4 sin x )
= (4 sin x)³ + 2
= 64 sin³ x + 2
(f ο g)(- 1/2 π) = 64 sin³(- 1/2 π ) + 2
= 64 (-1) + 2
= -62
13. Diketahui f:R→R , g:R→R dengan g(x)=2x + 5 dan (g ο f)(x)=12x² – 4x + 15. Berapakah nilai f(x)!
Jawaban :
g(x)=2x + 5
(g ο f)(x)=12x² – 4x + 15
g( f(x) ) = 12x² – 4x + 15
Karena g(x) = 2x + 5 maka:
2 f(x) + 5 = 12x² – 4x + 15
2 f(x) = 12x² – 4x + 19 – 5
2 f(x) = 12x² – 4x + 14
f(x) = 6x² – 2x + 7
14. Fungsi-fungsi f, g dan h adalah pemetaan dari R→R dengan f(x) = x + 2, g(x) = 4 – x dan h(x) = x²- x + 3. Tentukan berapa nilai ((f ο g) ο h)(x)!
Jawaban :
f(x)=x + 2
g(X)=4 – x
h(x)=x² – x + 3
((f ο g) ο h)(x) = ?
Misalkan (f ο g) = a
(f ο g)(x) = a(x)
f( g(x) ) = a(x)
f(4 – x) = a(x)
(4 – x) + 2 = a(x)
6 – x = a(x)
((f ο g) ο h)(x)=(a ο h)(x) = a( h(x) ) = a(x² – x + 3)
Karena
a(x) = 6 – x
maka
a(x² – x + 3) = 6 – (x² – x + 3) = 3 – x² + x
Jadi, ((f ο g) ο h)(x)=3 – x² + x
Dengan melihat beberapa contoh soal fungsi komposisi disertai dengan cara dan tahapan pengerjaannya, diharapkan para siswa bisa lebih mudah memahaminya. Sehingga, ketika guru memberikan soal ulangan mengenai materi tersebut, siswa dapat memperoleh nilai bagus.
Baca Juga :