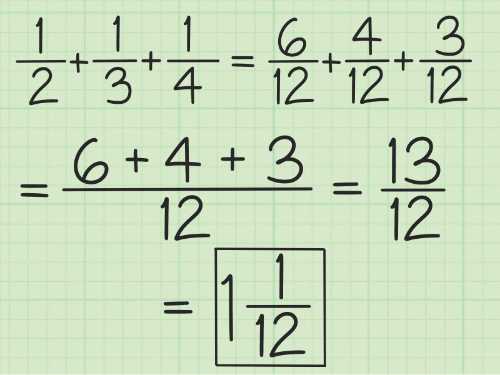Saat kamu sudah menginjak kelas 6, mungkin kamu ingin masuk di SMP idaman kamu. Ta[i sebelum itu, kamu juga harus bisa menguasai contoh soal Matematika kelas 6 SD semester 1 dan 2. Selain dari buku pelajaran, di internet juga banyak contoh soal untuk dipelajari.

Bukan cuma soal latihannya saja, ada rangkuman materi yang bisa kamu baca sebelum menjawab soal. Rangkuman materi ini akan membantu dalam mengingat rumus dan cara menyelesaikan soal-soal tertentu.

Kamu sedang mencari contoh-contoh soal untuk dipelajari sebelum ujian? Di bawah ini, kamu bisa melihat satu persatu dan mengerjakannya pelan-pelan. Kalau kamu banyak berlatih, nilai ulangan kamu pasti bagus. Jadi, selamat mencoba!

Contoh Soal Matematika Kelas 6 SD Semester 1 dan 2 tentang Operasi Hitung Campuran

Contents show

Operasi perhitungan terdiri dari penjumlahan, pengurangan, perkalian, dan pembagian. Operasi hitung campuran adalah operasi perhitungan yang melibatkan lebih dari satu operasi. Untuk melatih kemampuan pada materi ini, perhatikan contoh-contoh berikut!

1. Contoh Soal 1

Hasil dari -175 + (-125) – (-345) adalah …

Penyelesaian:

-175 + (-125) + 345

= (-300) + 345

= 45

2. Contoh Soal 2

Hasil dari 1.530 – 142 x 9 adalah …

Penyelesaian:

1.530 – (142 x 9)

= 1.530 – 1.278

= 252

3. Contoh Soal 3

Hasil dari 4 x 250 + 364 x 5 adalah …

Penyelesaian:

(4 x 250) + (364 x 5)

= 1.000 + 1.820

= 2.820

4. Contoh Soal 4

Hasil dari 594 : 54 x 5 adalah …

Penyelesaian:

(594 : 54) x 5

= 11 x 5

= 55

5. Contoh Soal 5

Hasil dari 54 x 6 + 63 : 7 adalah …

Penyelesaian:

(54 x 6) + (63 : 7)

= 324 + 9

= 333

Contoh Soal Matematika Kelas 6 SD Semester 1 dan 2 tentang Faktorisasi Prima

Bilangan prima adalah bilangan yang habis dibagi dengan satu dan bilangan itu sendiri. Faktor prima adalah bilangan prima yang bisa habis membagi suatu bilangan. Faktorisasi prima adalah perkalian bilangan-bilangan prima dari suatu bilangan.

1. Contoh Soal 1

2 x 3² x 5 x 7 adalah faktorisasi prima dari …

Penyelesaian:

2 x 3² x 5 x 7

= 2 x 9 x 5 x 7

= 18 x 35

= 630

2. Contoh Soal 2

2³ x 3 x 5² adalah faktorisasi prima dari …

Penyelesaian:

2³ x 3 x 5²

= 8 x 3 x 25

= 24 x 25

= 600

3. Contoh Soal 3

Faktorisasi prima dari 36 adalah …

Penyelesaian:

36 = 2 x 18 = 2 x 2 x 9 = 2 x 2 x 3 x 3 = 2² x 3³

4. Contoh Soal 4

Faktorisasi prima dari 125 adalah …

Penyelesaian:

125 = 5 x 25 = 5 x 5 x 5 = 5³

5. Contoh Soal 5

2 x 3³ x 5² adalah faktorisasi prima dari …

Penyelesaian:

2 x 3³ x 5²

= 2 x 27 x 25

= 1.350

Contoh Soal Ulangan Semester 1 Kelas 6 Matematika tentang KPK dan FPB

KPK (Kelipatan Persekutuan Terkecil) adalah kelipatan yang sama dari dua bilangan atau lebih yang mempunyai nilai terkecil. Sedangkan FPB (Faktor Persekutuan Terbesar) adalah bilangan yang dapat membagi habis dua bilangan atau lebih yang nilainya paling besar.

1. Contoh Soal 1

KPK dari 8 dan 9 adalah …

Penyelesaian:

Faktor 8 = 2 x 2 x 2 = 2³

Faktor 9 = 3 x 3 = 3²

KPK adalah hasil perkalian faktor-faktor yang sama dengan pangkat terbesar dengan faktor yang berbeda.

KPK = 2³ x 3² = 8 x 9 = 72

Jadi, KPK dari 8 dan 9 adalah 72.

2. Contoh Soal 2

FPB dari 15 dan 25 adalah …

Penyelesaian:

Faktor 15 = 3 x 5

Faktor 25 = 5 x 5 = 5²

FPB adalah hasil perkalian faktor yang sama dengan pangkat terkecil

FPB = 5.

Maka, Faktor Persekutuan Terbesar dari 15 dan 25 ialah 5.

3. Contoh Soal 3

KPK dari 12 dan 36 adalah …

Penyelesaian:

Faktor 12 = 2 x 6 = 2 x 2 x 3 = 2² x 3

Faktor 36 = 2 x 18 = 2 x 2 x 9 = 2 x 2 x 3 x 3 = 2² x 3²

KPK = 2² x 3² = 4 x 9 = 36

Maka, KPK dari 12 dan 36 adalah 36.

4. Contoh Soal 4

FPB dari 18 dan 27 adalah …

Penyelesaian:

Faktor 18 = 2 x 9 = 2 x 3 x 3 = 2 x 3²

Faktor 27 = 3 x 9 = 3 x 3 x 3 = 3²

FPB = 3² = 9

Maka, FPB dari 18 dan 27 adalah 9.

5. Contoh Soal 5

KPK dari 5 dan 15 adalah …

Penyelesaian:

Faktor 5 = 5

Faktor 15 = 3 x 5

KPK = 3 x 5 = 15

Jadi, KPK dari 5 dan 15 adalah 5.

Contoh Soal Matematika Kelas 6 SD Semester 1 dan 2 tentang Lingkaran

Lingkaran adalah bangun datar yang memiliki satu sisi dan membentuk sudut 180 derajat. Rumus menghitung keliling lingkaran adalah 2 x phi x r atau 2 x phi x d/2. Sedangkan rumus menghitung luas lingkaran adalah phi x r².

1. Contoh Soal 1

Busur dan dua buah jari-jari membatasi bagian lingkaran yang bernama …

Tembereng
Juring
Tali busur
Apotema

Jawaban: B

2. Contoh Soal 2

Bagian apa yang membatasi tembereng pada sebuah lingkaran?

Jari-jari dan diameter
Busur dan tali busur
Tali busur dan apotema
Jari-jari dan busur

Jawaban: B

3. Contoh Soal 3

Sebuah lingkaran mempunyai jari-jari 30 cm. Berapa diameter lingkaran tersebut? …

Penyelesaian:

Diameter lingkaran = 2 x jari-jari lingkaran

Diameter = 2 x 30 cm = 60 cm

Jadi, diameter lingkaran itu ialah 60 cm.

4. Contoh Soal 4

Diketahui jari-jari sebuah lingkaran adalah 14 cm. Berapa luas dan keliling lingkaran itu?

Penyelesaian:

Luas lingkaran = phi x r²

= 22/7 x 14 cm x 14 cm

= 616 cm^2

Keliling lingkaran = 2 x phi x r

= 2 x 22/7 x 14 cm

= 2 x 22/7 x 14

= 88 cm

Maka, keliling dan luas lingkaran tersebut adalah 616 cm² dan 88 cm.

5. Contoh Soal 5

Sebuah lingkaran memiliki luas 314 cm². Berapa jari-jarinya?

Penyelesaian:

Luas lingkaran = phi x r²

314 cm² = 3,14 x r²

r² = 314 : 3,14

r² = 100

r = 10 cm

Maka, jari-jari lingkaran itu adalah 10 cm.

Contoh Soal Matematika Kelas 6 SD Semester 1 dan 2 tentang Pecahan Desimal

Pecahan desimal adalah pecahan yang berbentuk bilangan dengan koma. Pecahan desimal juga bisa disebut sebagai hasil perhitungan dari pecahan biasa. Pecahan dihitung dengan membagi angka pembilang dengan angka penyebut.

Soal tentang pecahan desimal berbeda dengan soal bilangan bulat. Kamu bisa latihan menjawab soal pecahan desimal dengan soal-soal di bawahi ini.

1. Contoh Soal 1

Nilai pecahan dari 0,50 adalah …

Penyelesaian:

0,50 = 50/100

50/100 disederhanakan menjadi 1/2

Maka, nilai pecahannya adalah 1/2.

2. Contoh Soal 2

4/6 … 8/12

Apa tanda yang tepat untuk mengisi titik-titik tersebut?

Penyelesaian:

Dengan menyamakan penyebut 4/6, diperoleh nilai 8/12.

Maka, 4/6 = 8/12.

3. Contoh Soal 3

25% dari 160 adalah …

Penyelesaian:

25% x 160 = 25/100 x 160 = 1/4 x 160 = 40.

Maka, 25% dari 160 ialah 40.

4. Contoh Soal 4

3/4 pada bagian pepaya yang utuh memiliki berat 1,5 kg. Berat pepaya yang masih utuh adalah …

Penyelesaian:

Berat 1/4 bagian = 1,5 kg : 3 = 15/10 : 3/1 = 15/10 x 1/3 = 5/10 = 0,5 kg.

Berat satu bagian = 3/4 bagian + 1/4 bagian = 1,5 kg + 0,5 kg = 2 kg.

Maka, berat pepaya yang masih utuh adalah 2 kg.

5. Contoh Soal 5

Jumlah murid SD Harapan Jaya adalah 830 anak. Murid perempuan ada 2/5 bagian. Berapa banyak anak murid laki-laki?

Penyelesaian:

Banyak murid perempuan = 2/5 x 830 = 332 anak.

Banyak murid laki-laki = 830 – 332 = 498 anak.

Jadi, jumlah siswa laki-laki adalah 498 orang.

Contoh Soal Matematika Kelas 6 SD Semester 1 dan 2 tentang Operasi Hitung Pecahan

Operasi hitung pecahan biasanya melibatkan dua buah pecahan atau lebih. Dalam penjumlahan dan pengurangan, kamu harus terlebih dahulu menyamakan penyebut semua pecahan. Dalam perkalian, sesama pembilang dan sesama penyebut bisa langsung dikalikan.

Dalam pembagian, pecahan yang membagi harus dibalik terlebih dahulu. Pembilang menjadi penyebut, dan penyebut menjadi pembilang. Kemudian, tanda bagi diubah menjadi kali. Pelajari lebih jauh contoh latihan dari bank soal kelas 6 berikut ini.

1. Contoh Soal 1

1/5 + 3/8 = …

Penyelesaian:

1/5 + 3/8 (samakan penyebut menjadi 40)

= 8/40 + 15/40

= 23/40

2. Contoh Soal 2

3/4 – 1/3 = …

Penyelesaian:

3/4 – 1/3 (samakan penyebut menjadi 12)

= 9/12 – 4/12

= 5/12

3. Contoh Soal 3

5/4 x 16/3 = …

Penyelesaian:

5/4 x 16/3

= 5/1 x 4/3

= 20/3

= 6 2/20

= 6 1/10

4. Contoh Soal 4

2 3/4 : 3/8 = …

Penyelesaian:

2 3/4 : 3/8

= 11/4 x 8/3

= 11/1 x 2/3

= 22/3

= 7 1/3

5. Contoh Soal 5

2/4 + 1/3 – 3/12 = …

Penyelesaian:

2/4 + 1/3 – 3/12 (samakan penyebut menjadi 12

= 6/12 + 4/12 – 3/12

= 10/12 – 3/12

= 7/12

Contoh Soal Bangun Ruang Kelas 6 SD

Bangun ruang adalah bangun tiga dimensi yang mempunyai ruang di dalamnya. Contoh bangun ruang adalah balok, kubus, limas, bola, prisma, tabung, kerucut, dan lain-lain.

1. Contoh Soal 1

Sebuah kubus mempunyai panjang rusuk 8 cm. Berapa luas permukaan kubus tersebut?

Penyelesaian:

Luas permukaan kubus = 6 x s²

= 6 x 8²

= 6 x 64

= 384 cm²

Maka, luas permukaan kubus adalah 384 cm².

2. Contoh Soal 2

Volume sebuah kubus adalah 216 cm³. Berapa panjang rusuk kubus tersebut?

Penyelesaian:

Volume kubus = s³

216 cm^3 = s³

s = 6 cm

Maka, panjang rusuk kubus tersebut ialah 6 cm.

3. Contoh Soal 5

Sebuah limas segitiga mempunyai luas alas 75 cm² dan tinggi limas adalah 5 cm. Berapa volume limas segitiga tersebut?

Penyelesaian:

Volume limas segitiga = 1/3 x luas alas x tinggi

= 1/3 x 75 x 5

= 125 cm³

Jadi, volume limas segitiga tersebut adalah 125 cm³.

4. Contoh Soal 4

Sebuah tabung memiliki jari-jari alas 7 cm dan tinggi 5 cm. Berapa luas permukaan dan volume tabung tersebut?

Penyelesaian:

Luas permukaan tabung = 2 x phi x r (r + t)

= 2 x 22/7 x 7 (7 + 5)

= 44 (12)

= 528 cm²

Volume tabung = phi x r² x t

= 22/7 x 7² x 5

= 22/7 x 49 x 5

= 770 cm³

Maka, luas permukaan dan volume tabung tersebut adalah 528 cm^2 dan 770 cm^3.

5. Contoh Soal 5

Sebuah prisma memiliki alas persegi panjang. Ukuran setiap alas adalah 10 cm x 5 cm. Tinggi prisma adalah 9 cm. Volume prisma tersebut adalah …

Penyelesaian:

Volume prisma = luas alas x tinggi

= luas persegi panjang x tinggi

= 10 cm x 5 cm x 9 cm

= 450 cm³

Jadi, volume prisma adalah 450 cm³.

Contoh Soal Matematika Kelas 6 SD Semester 1 dan 2 tentang Menghitung Skala

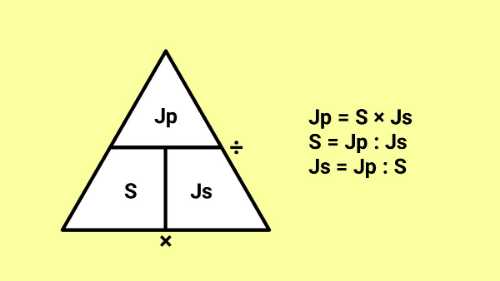
Skala adalah perbandingan jarak pada peta terhadap jarak sebenarnya. Rumus menghitung skala adalah jarak pada peta : jarak sebenarnya. Rumus jarak pada peta adalah skala x jarak sebenarnya. Rumus jarak sebenarnya adalah jarak pada peta : skala.

1. Contoh Soal 1

Jarak Kota A dan B pada gambar adalah 12 cm. Jarak sebenarnya kedua kota itu adalah 60 km. Berapa skala gambar?

Penyelesaian:

Skala = jarak pada peta : jarak sebenarnya

= 12 cm : 60 km

= 12 : 6.000.000

= 1 : 500.000

Maka, skala gambar itu adalah 1 : 600.000.

2. Contoh Soal 2

Jarak kedua kota pada peta adalah 7 cm. Jika skala peta adalah 1 : 300.000, jarak sebenarnya kedua kota itu adalah …

Penyelesaian:

Jarak sebenarnya = jarak pada peta : skala

= 7 cm : (1 : 300.000)

= 7 x 300.000

= 2.100.000 cm

= 21 km

3. Contoh Soal 3

Jarak sebenarnya antara Kota C dan D adalah 18 km, skala peta adalah 1 : 200.000. Berapa jarak kedua kota pada peta?

Penyelesaian:

Jarak pada peta = skala x jarak sebenarnya

= 1 : 200.000 x 18 km

= 1 : 200.000 x 1.800.000

= 9 cm

Maka, jarak kedua kota itu di peta ialah 9 cm.

4. Contoh Soal 4

Pada peta, tertera skala 1 : 15.000. Jika jarak Kota B dan C pada peta adalah 8 cm, maka jarak sebenarnya adalah …

Penyelesaian:

Jarak sebenarnya = jarak pada peta : skala

= 8 cm : (1 : 15.000)

= 8 x 15.000

= 120.000 cm

= 1,2 km

Jadi, jarak sebenarnya Kota B dan C adalah 1,2 km.

5. Contoh Soal 5

Jarak pada peta antara Kota F dan G ialah 2 cm. Jika jarak sebenarnya adalah 120 km, maka skala peta tersebut adalah …

Penyelesaian:

Skala = jarak pada peta : jarak sebenarnya

= 2 cm : 120 km

= 2 cm : 12.000.000

= 1 : 6.000.000

Maka, skala peta itu adalah 1 : 6.000.000.

Contoh Soal Matematika Kelas 6 Semester 1 Dan Kunci Jawaban tentang Rata-Rata, Median, dan Modus

Rata-rata adalah hasil pembagian seluruh jumlah nilai dengan banyak data. Median adalah nilai tengah dari suatu data. Modus adalah nilai yang paling banyak muncul di suatu data. Perhatikan contoh soal berikut agar kamu lebih paham tentang materi ini.

1. Contoh Soal 1

Nilai hasil ulangan Bahasa Indonesia dari 10 siswa ialah sebagai berikut.

8, 7, 6, 9, 6, 8, 7, 7, 9, 8

Median data tersebut adalah …

Penyelesaian:

Urutan data = 6, 6, 7, 7, 7, 8, 8, 8, 9, 9

Median = data ke (n+1)/2 = data ke (10+1)/2 = data ke 11/2 = data ke 5,5

Maka, median dari data itu adalah 7,5.

2. Contoh Soal 2

Pelemparan dadu sebanyak 10 kali, angka yang keluar ialah:

1 5 4 2 3 4 1 2 4 6

Modus dari data tersebut adalah …

Penyelesaian:

Banyak dadu 1 keluar: 2 kali

Banyak dadu 2 keluar: 2 kali

Banyak dadu 3 keluar: 1 kali

Banyak dadu 4 keluar: 3 kali

Banyak dadu 5 keluar: 1 kali

Banyak dadu 6 keluar: 1 kali

Jadi, modus data itu adalah 4.

3. Contoh Soal 3

Hasil ulangan IPS siswa kelas 6 ialah sebagai berikut.

6, 8, 7, 9, 10, 7, 10, 9, 6, 9, 7, 9, 6, 8, 7, 7, 7, 9, 10, 8

Nilai rata-ratanya adalah …

Penyelesaian:

Rata-rata = jumlah nilai : banyak data

= (6 + 8 + 7 + 9 + 10 + 7 + 10 + 9 + 6 + 9 + 7 + 9 + 6 + 8 + 7 + 7 + 7 + 9 + 10 + 8) : 20

= 159 : 20

= 7,95

Maka, nilai rata-rata data tersebut adalah 7,95.

4. Contoh Soal 4

Dalam suatu data nilai ulangan IPA tertulis: 80, 70, 70, 50, 70, 50, 60, 70, 50, 90.

Modus dari data tersebut ialah …

Penyelesaian:

Banyak data 50: 2

Banyak data 60: 1

Banyak data 70: 4

Banyak data 80: 1

Banyak data 90: 1

Maka, modusnya adalah 70.

5. Contoh Soal 5

Nilai ulangan Bahasa Inggris 5 siswa adalah sebagai berikut.

80, 70, 95, 85, 90

Berapa rata-ratanya?

Penyelesaian:

Rata-rata = jumlah nilai : banyak data

= (80 + 70 + 95 + 85 + 90) : 5

= 420 : 5

= 84

Maka, rata-rata nilai ulangan adalah 84.

Contoh Soal Matematika SD Kelas 6 Semester 1 tentang Debit

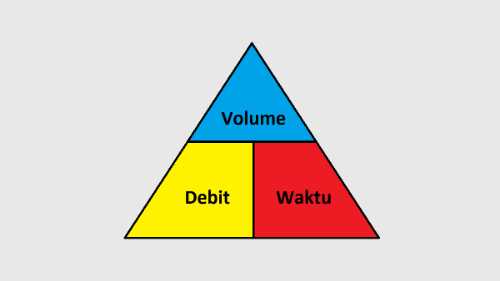
Debit adalah volume air yang mengalir selama waktu tertentu. Rumus menghitung debit adalah volume : waktu. Volume dapat menggunakan satuan liter atau m³. Sedangkan satuan waktu yang bisa dipakai adalah jam, menit, dan detik.

1. Contoh Soal 1

Debit keran air pada bak mandi ialah 1,5 m³/detik. Berapa banyak air yang ditampung dalam waktu 3 menit?

Penyelesaian:

Debit = volume : waktu

1,5 m³/detik = volume : 3 menit

1,5 = volume : 180 detik

Volume = 1,5 x 180 = 270

Maka, banyak air yang ditampung selama tiga menit adalah 270 m³.

2. Contoh Soal 2

Volume air yang keluar dari suatu pipa dalam waktu 5 menit ialah 900 liter. Debit air tersebut adalah …

Penyelesaian:

Debit = volume : waktu

= 900 liter : 5 menit

= 180

Jadi, debit air tersebut adalah 180 liter/menit.

3. Contoh Soal 3

Selang dari mobil pemadam kebakaran menyemprotkan air selama 15 menit. Persediaan air yang dibawa berkurang dari 6.500 liter menjadi 5.000 liter. Debit air yang berkurang adalah …

Penyelesaian:

Volume air yang berkurang = 6.500 – 5.000 = 1.500 liter.

Debit = volume : waktu

= 1.500 : 15

= 100

Maka, debit air yang berkurang ialah 100 liter/menit.

4. Contoh Soal 4

Sebuah ember berisi air sebanyak 620 m³. Karena ember tersebut bocor, air berkurang dan tersisa 100 m³ dalam waktu 40 menit. Debit air yang berkurang adalah … m³/menit.

Penyelesaian:

Volume air yang berkurang = 620 – 100 = 520 m³

Debit = volume : waktu

= 520 : 40

= 13

Jadi, debit air yang berkurang ialah 13 m³/menit.

5. Contoh Soal 5

Sebuah tabung memiliki volume 20 m³. Tabung tersebut akan dialiri air dengan debit 100 m³/menit. Tabung itu akan penuh dalam waktu … detik.

Penyelesaian:

Debit = volume : waktu

100 = 20 : waktu

Waktu = 0,2 menit = 0,2 x 60 = 12

Maka, tabung akan penuh selama 12 detik.

Sudah sejauh apa kamu memahami materi-materi di atas? Dengan menjawab Contoh soal Matematika kelas 6 SD semester 1 dan 2 tersebut, kamu akan semakin mengerti jika berhadapan dengan soal-soal yang mirip. Jangan lupa untuk terus berlatih!