Desacanggu.id – Jika saat ini kamu duduk di bangku sekolah tingkat SMP atau SMA, maka materi pelajaran tentang transformasi geometri menjadi salah satu yang akan ditemui, khususnya kelas 9 dan 11. Bisa dikatakan jika pembahasan tentang materi ini berkaitan dengan perubahan sebuah bidang.

Bahkan sebenarnya dalam kehidupan sehari-hari pun sangat mudah menemukan transformasi ini. Sementara kalau di pelajaran matematika, kamu akan menemukannya dalam bentuk titik-titik tertentu. Untuk lebih memahami materi tentang geometri ini, silakan simak ulasan di bawah ini sampai selesai.

Pengertian Transformasi Geometri

Contents show

Secara umum, transformasi sering diartikan sebagai sebuah bentuk perubahan, bisa berupa sifat, rupa atau bahkan struktur lain yang akan mengubah dengan cara menambah atau mengurangi, dan menata kembali unsur-unsur yang ada di dalamnya. Lantas, apa arti dari geometri?

Geometri sendiri bisa diartikan sebagai sebuah ilmu ukur yang merupakan salah satu cabang dalam matematika, khususnya menjelaskan tentang sudut, sifat garis serta bidang dan ruang. Dari pengertian dua kata di atas, apakah kamu sudah bisa menyimpulkan pengertian dari istilah tersebut?

Secara sederhana, istilah tersebut bisa diartikan sebagai sebuah perubahan yang terjadi pada sebuah sudut, garis, bidang maupun ruang. Adapun bidang yang sering menerapkan transformasi bangun geometri antara lain adalah desain arsitektur, karya seni dan lain sebagainya.

Bisa dikatakan bahwa fungsi dari transformasi tersebut paling banyak diaplikasikan dalam bidang permesinan, seni, arsitektur, televisi dan juga film. Sampai di sini, apakah kamu sudah memiliki gambaran tentang materi yang akan dipelajari? Biar tidak bingung ikuti pembahasannya di bawah ini.

Jenis-jenis Transformasi Geometri

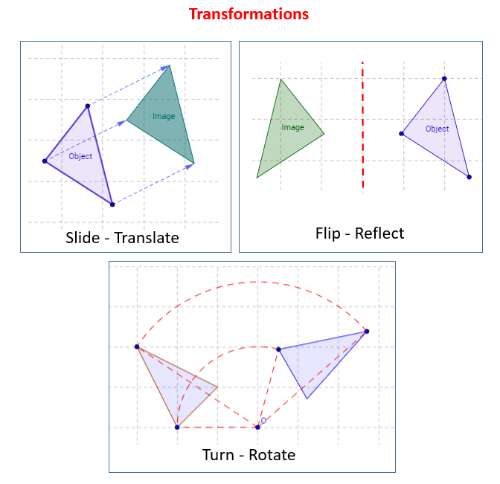
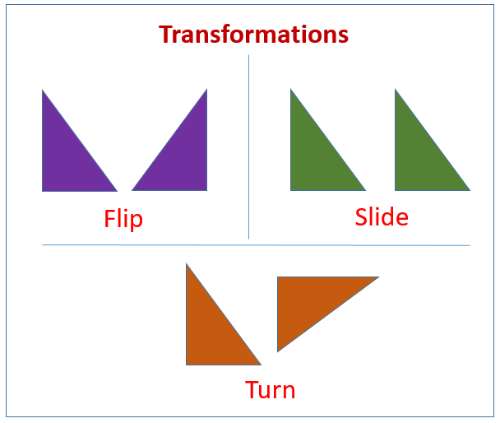
Transformasi bangun dan bidang geometri bisa dibedakan menjadi 4 jenis. Yaitu translasi, refleksi, rotasi dan dilatasi. Bagaimana penjelasan dari keempat jenis transformasi tersebut, berikut adalah pemaparannya secara lengkap.

1. Transformasi Geometri Translasi

Jenis transformasi ini juga dikenal dengan pergeseran yang ditunjukkan dengan adanya pergeseran atau perpindahan dari satu titik menuju ke arah titik lainnya namun masih berada dalam satu garis lurus bidang datar.

Dengan adanya pergeseran tersebut maka bisa mengakibatkan pergeseran pada bidang lainnya yang berada di garis lurus tersebut. Jedi bidang akan bergeser sesuai dengan jarak dan arah tertentu.

Dapat dikatakan bahwa pada dasarnya translasi ini hanya akan mengubah posisi karena adanya pergeseran dan bukan mengubah bentuk apalagi ukuran bidang. Apa saja contoh dari penerapan translasi dalam kehidupan sehari-hari?

Contoh sederhananya adalah kendaraan yang melaju ke arah lurus, hal ini menunjukkan adanya pergeseran atau perpindahan tanpa menyebabkan perubahan bentuk dan ukuran. Jadi kendaraan hanya berpindah tempat saja.

Contoh lainnya adalah perosotan. Jika ada anak-anak yang bermain perosotan maa hal itu menunjukkan bahwa telah terjadi transformasi translasi karena anak-anak tersebut akan berpindah posisinya dari mulai di titik awal hingga sampai ke ujung perosotan.

Rumus pada translasi adalah seperti berikut:

x’,y’ = (a.b) + (x,y)

Keterangan:

x’,y’ adalah titik bayangan

xy adalah titik asal

a,b adalah vektor translasi

Contoh soal:

Tentukan titik bayangan jika titik A adalah (3,5) dan ditranslasikan menjadi (7,4).

Jawab:

x’y’ = (x+a, y+b)

(x’y) = (3+7, 5+4)

(x’y’) = (10,9)

Jadi titik bayangannya ada di (10,9)

2. Transformasi Geometri Refleksi

Jenis selanjutnya adalah refleksi atau pencerminan. Pada jenis transformasi bidang atau bangun geometri ini terjadi perubahan dengan adanya perpindahan titik dari sifat cermin datar. Pada jenis transformasi ini terdapat dua sifat yang perlu diperhatikan, yaitu:

Jarak dari titik ke cermin sama dengan jarak dari bayangan titik ke cermin.
Bidang geometri atau bangun geometri yang dicerminkan saling berhadapan antara satu dengan yang lain.

Contoh paling sederhana dari penerapan jenis transformasi refleksi pada geometri ini adalah saat kita sedang bercermin. Atau bisa juga berupa pantulan bayangan dari objek tertentu yang terlihat di permukaan air.

Rumus transformasi geometri refleksi ada beberapa macam, diantaranya adalah seperti berikut:

Refleksi terhadap sumbu	Maka titik bayangannya
Refleksi terhadap sumbu -x : (x,y)	(x,-y)
Refleksi terhadap sumbu -y : (x,y)	(-x,y)
Refleksi terhadap garis y = -x : (x,y)	(-y,x)
Refleksi terhadap garis y = x : (x,y)	(y,x)
Refleksi terhadap garis y = h : (x,y)	(2h,-x,y)
Refleksi terhadap garis y = k : (x,y)	(x,2k-y)

Contoh soal transformasi refleksi:

Tentukanlah koordinat bayangan dari titik A, jika titik A (5,-3) dicerminkan terhadap sumbu x.

Jawab:

A : (a,b) maka A’ (a,-b)

A (5,-3) maka A’ (-5,-3)

Jadi titik bayangan dari A ada di (-5,-3).

3. Transformasi Geometri Rotasi

Jenis transformasi rotasi ini bisa dikatakan sebagai perputaran. Yang artinya sebuah perputaran dari suatu bidang ditentukan oleh letak titik rotasinya, sudut rotasi serta arah perputaran atau rotasinya.

Prinsipnya yaitu memutar terhadap titik pusat dan sudut yang jaraknya sama dengan titik yang mengalami rotasi atau diputar. Karena sifatnya hanya berputar saja, maka transformasi bidang geometri tersebut tidak akan mengubah bentuk maupun ukuran dari bidangnya.

Sudut rotasi pada suatu benda bisa searah jarum jam atau berlawanan dengan jarum jam. Hal ini juga akan berpengaruh terhadap nilai dari sudut rotasi seperti berikut ini:

Sudut rotasi akan bernilai (+) jika arah putarannya berlawanan dengan arah jarum jam.
Sudut rotasi akan bernilai (-) jika arah perputarannya searah dengan jarum jam.

Contoh sederhana dari transformasi rotasi bisa kamu lihat pada wahana permainan bianglala yang berputar. Dimana lingkaran akan memutari titik pusat yang berada di tengah. Contoh lainnya adalah gangsing yang berputar.

Pada transformasi ini, rumus rotasi terdiri dari beberapa macam, diantaranya adalah seperti berikut:

Rotasi sebuah bidang	Maka titik rotasinya
Rotasi 90^o dengan pusat (a,b) : (x,y)	(-y + a + b, x – a + b)
Rotasi 180^o dengan pusat (a,b) : (x,y)	(-x -2a, -y +2b)
Rotasi -90^o dengan pusat (a,b) : (x,y)	(y – b + a, -x + a+ b)
Rotasi 90^odengan pusat (0,0) : (x,y)	(-y,x)
Rotasi 180^o dengan pusat (0,0) : (x,y)	(-x,-y)
Rotasi 90^odengan pusat (0,0) : (x,y)	(y,-x)

Contoh soal transformasi bangun dan bidang geometri rotasi:

Jika sebuah titik A (-4,-3) dirotasikan terhadap titik lainnya yakni O (0,0) sebesar 90^oberlawanan dengan jarum jam, maka tentukanlah titik koordinat bayangan dari titik A tersebut.

Jawab:

(x’,y’) = (-y,x)

(x’,y) = (-4,-3)

(-y,x) = (3,-4)

Jadi titik bayangan rotasi A berada di titik (3,-4).

4. Transformasi Geometri Dilatasi

Berbeda dari jenis transformasi bangun dan bidang geometri lainnya, transformasi dilatasi yang disebut juga dengan perkalian ini akan menimbulkan terjadinya perubahan ukuran. Dalam transformasi ini terdapat dua prinsip, yaitu titik serta faktor dilatasi.

Titik dilatasi akan menentukan posisi dilatasi tersebut dan menjadi tempat pertemuan yang menghubungkan semua garis lurus antara titik bidang ke titik yang menjadi hasil dilatasi.
Faktor dilatasi merupakan faktor perkalian dari sebuah bangun geometri yang sudah mengalami dilatasi.

Adapun sifat-sifat dari transformasi dilatasi adalah seperti berikut:

Dilatasi akan menyebabkan ukuran sebuah bangun geometri berubah, kecuali pada faktor skala k = 1 yang ukuran memiliki ukuran benda tetap. Dengan demikian perubahan ukuran pada sebuah bangun akan dipengaruhi besarnya faktor skala k, yang terbagi menjadi:

Jika skala k > 1 maka sebuah bangun akan diperbesar dengan letak searah pusat dilatasi dari bangun semula.
Jika skala k = 1 maka sebuah bangun tidak akan mengalami perubahan ukuran maupun letak.
Jika 0 < k < 1 maka sebuah bangun akan diperkecil dan letaknya searah terhadap pusat dilatasi dari bangun semula.
Jika -1 < k < 0, maka sebuah bangun akan diperkecil dan letaknya berlawanan terhadap pusat dilatasi dari bangun semula.
Jika skala k = -1 maka sebuah bangun tidak akan mengalami perubahan ukuran dan letaknya berlawanan dengan pusat dilatasi dari bangun semula.
Jika skala k < -1 maka sebuah bangun akan diperbesar dan letaknya berlawanan dengan pusat dilatasi dari bangun semula.

Contoh sederhana dari transformasi dilatasi adalah miniatur bangunan yang merupakan bentuk kecil dari sebuah bangunan yang dijadikan miniatur tersebut. Selain itu juga bisa berupa ukuran foto yang berbeda-beda seperti 2×3, 3×4 yang gambarnya tetap sama namun ukurannya beda.

Adapun rumus umum yang sering diterapkan pada transformasi dilatasi adalah seperti berikut:

Dilatasi dengan titik pusat O(0,0) dan faktor skala k: (x,y) à (kx,ky)
Dilatasi dengan titik pusat (0,0) dan faktor skala k : (x,y) à (kx = k(x-a) + a, (k(y-b) + b)

Contoh soal:

Koordinat bayangan titik B (12,-9) didilatasi terhadap titik pusat O dengan faktor skala -1/3 adalah…

Jawab:

Rumus A(x,y) didilatasi terhadap pusat (0,0) faktor skala k titik asal (x,y) maka hasilnya adalah A’(kx,ky).

B’ = (-1/3 x 12), (-1/3x-9)

= (-4,3)

Jadi titik B (12,-9) didilatasi terhadap titik pusat O dengan faktor skala -1/3 hasilnya adalah B’ adalah (-4,3).

Bagaimana, sampai di sini apakah kamu sudah semakin paham dengan pembahasan tentang transformasi bidang dan bangun geometri?

Contoh Transformasi Geometri dalam Kehidupan Sehari-hari

Sebagai salah satu materi yang dipelajari dalam pelajaran matematika, tentu ada banyak contoh penerapannya dalam kehidupan sehari-hari. Lantas apa saja yang contoh dari transformasi bidang dan bangun geometri dalam kehidupan sehari-hari?

Contoh sederhana dari transformasi bidang dan bangun geometri adalah dua orang yang bermain catur, dimana masing-masing pemain akan memindahkan bidak pada papan catur ke posisi yang paling tepat.

Contoh lainnya bisa dilihat dari permainan bianglala yang berputar dan menunjukkan rotasi dengan arah yang berlawanan dengan jarum jam atau searah dengan jarum jam. Sementara untuk refleksi sudah disinggung di awal, contoh sederhananya adalah ketika kita bercermin di cermin datar.

Bagaimana dengan dilatasi? Seperti yang diketahui, dilatasi menunjukkan adanya perubahan pada ukuran namun tidak pada bentuknya. Seperti pada miniatur bangunan, mainan mobil-mobilan dan lain sebagainya.

Setelah mengetahui dan mempelajari materi tentang apa itu transformasi geometri beserta jenis, rumus serta contoh sederhananya, tentunya kamu jadi lebih memahami tentang materi tersebut. Dari pembahasan di atas, bagian mana yang masih belum kamu pahami?